And accept "c" as a slider or {sqrt(c² y² z²), sqrt(c² y²And 4z to get x2 = y2 = z2 = 2 Since x2 y2 z2 = 3 2 = 1, we get = 2 3 and thus each of x;y;z is p1 3Mar 16, 07 · (x y)^2 = x^2 2xy y^2 Earlier, when I put x^2 2xy y^2 is the bracket, I meant to keep it away from z^2 so that the factoring would be clearer for you Sorry I confused you instead I think what you didn't get was the x^2 and y^2 in the bracket and the appearence of (x y)^2 in the next step (x^2 y^2) = (x y)^2 is a wrong

Solved Let F X Y Z 1 X 2 Y 2 Z 2 Find The Domai Chegg Com
F(x y z)=xy^2z x^2+y^2+z^2=4
F(x y z)=xy^2z x^2+y^2+z^2=4-X^2y^2z^2=xyyzzx eq(1) Identity is x^3y^3z^3 3xyz=(xyz)(x^2y^2z^2xyyzzx) x^3y^3z^3 3xyz =(xyz)(xyyzzxxyyzzx) (acc to eq1) Therefore , x^3y^3z^3 3xyz = 0 So, x^3y^3z^3= 3xyz Answer read moreThen f(z) = z jzj2 = x x2 y2 i y x2 y2;



Solved Problem 1 12 Points Let F X Y X2 Y2 A F Chegg Com
Then, ∂ f ∂ x = x x 2 y 2 z 2, ∂ f ∂ y = y x 2 y 2 z 2, ∂ f ∂ z = z x 2 y 2 z 2 Okay, so now let's find a directional derivative!Jun 23, 15 · Suppose f(x,y,z)=x^2y^2z^2 and W is the solid cylinder?May 07, 19 · If 1/x 1/y 1/z = 1, show that the minimum value of the function a^3x^2 b^3y^2 c^3z^2 is (a b c)^3 asked May 8, 19 in Mathematics by Nakul (
WolframAlpha brings expertlevel knowledge and capabilities to the broadest possible range of people—spanning all professions and education levelsIf cos(xyz) = 1 x 2 y 2 z 2, find ∂ z ∂ x and ∂ z ∂ y check_circle Expert Solution Want to see the full answer?Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and
F(x,y,z) = x^2 y^2z^2 Subject to the constraints xy=1, y^2z^2 =1 It seems to me that z does not exist so there are no answers Is that correct?(a) If f(z) = 1 z;1 (Exercise 12) Find the maximum and minimum of f(x;y;z) = x4 y4 z4 subject to the constraint x 2y2 z = 1 Solution We have ∇f(x;y;z) = 4x3;4y3;4z3 = 2 x;2 y;2 z = ∇g(x;y;z) Case 1 If all of x;y;z ̸= 0, we can divide 4x3 = 2 x, 4y3 = 2 y, 4z3 = 2 z by 4x;4y;



Solved Problem 1 12 Points Let F X Y X2 Y2 A F Chegg Com



Extremes Of F X Y Z X 1 2y 2 Z 1 2 With X 2 Y 2 Z 2 Leq 1 Mathematics Stack Exchange
Let f(x,y,z) =x2−y2−z2 f ( x, y, z) = x 2 − y 2 − z 2 and let S be the level surface defined by f (x,y,z) = 4 (a) Find an equation for the plane tangent to S at P 0(1,−1,−2) P 0Then click on the marble of the row 2 ==> using the input bar x^2y^2z^2=c;We think you wrote (2xy3z2xy^2z/(x^2yy^2zxz^2))*x^2yy^2zxz^2 This deals with adding, subtracting and finding the least common multiple



Lagrange S Linear Equation Method Of Multipliers Mathematics Stack Exchange



Vector Analysis By Alimkanwalimtinaa Issuu
Multivariable calculus If $F=(x^2,y^2,z^2),S=\{x^2y^2z^2=1,z\geq 0\}$, evaluate $\iint_S F dS$ Mathematics Stack Exchange I'm having trouble computing this In spherical coordinates we get$$\int_0^{2\pi}\int_0^{\pi/2}\sin^4\theta\cos^3\phi\sin^4\theta\sin^3\phi\cos^3\theta\sin\theta d\theta d\phi \tag 1$$which isMinimize f(x, y, z) = x^2 y^2 z^2 subject to 4x^2 2y^2 z^2 = 4 Maximum Valua At (,,) (1 pt) Find the coordinates of the point (x, y, z) on the plane z = 2 x 2 y 3 which is closest to the origin x = 2 y = z =3dprinting, solidworks f(0,0,0) is 0, not 1 (the isosurface level), so you only get points drawn completing the cones if there are enough points near the origin that happen to have value 1 But when you switch to linspace(,,), the closest coordinates to the origin are at about 105, leaving a gap of about 21 between adjacent



2a Ex7 1314with Sol Tutorial Work With Full Detailed Solutions Studocu



14 2 Limits And Continuity
2 share Report Save Continue this threadThe same idea applies, the term under the square root can't be negative, ie 25x 2y 2z 2 >=0 1 share Report Save level 2 5 years ago So 25>(x,y,z)>0 as xyz can't be less than zero, and if they're greater than 25 than the entire function becomes less than 0 Would that be a suitable answer?More_vert Find the minimum value of f ( x , y , z ) = x 2 2 y 2 3 z 2 subject to the constraint x 2 y 3 z = 10 Show that f has no maximum value with this constraint



Copyright C Cengage Learning All Rights Reserved Ppt Download



Homework 14 5
May 08, 19 · Let F = (x 2 y 2 z 2) λ (x y z) We form the equations Fx = 0, F y = 0, Fz = 0 ie, 2x λ = 0, 2y λ = 0, 2z λ = 0 or λ = – 2x, λ = – 2y, λ = – 2z ⇒ – 2x = – 2y = – 2z or x = y = z But x y z = 3a Substituting y = z = x, we get 3x = 3a x = a ∴ x = a, y = a, z = a The required minimum value of x 2Letf (x,y,z) = x^2y^2z^2 Calculate the gradient of f Calculate ∫_C (F dr ) where F (x,y,z)= (x,y,z) and C is the curve parametrized by r (t)= (3cos^3 (t), 2sin^5 (t), 2cos^13 (t) for 2π≤t≤3πJun 22, 16 · a) If for this point the restrictions are obeyed, consider this as a successful one 4)Given de box volume V_b the total number of trials N and de number of successful trials n_s the area/volume is computed as v = (V_b/N) xx n_s In this case we have the restrictions defining the sought volume f(x,y,z) = x^2y^2z^2 = 2



Pde Tutorial Sheet



Solved 1 Point Suppose F X Y Z X2 Y2 Z2 And W Chegg Com
{eq}\displaystyle f(x,y,z) = (x^2 y^2 z^2)^{\frac{1}{2}} \\ P(x,y,z) = (2, 1, 2) \\ \vec{R} = \hat{i} 2 \hat{j} \hat{k} \\ \begin{align} \vec{R} &= \sqrt{1^2(2)^2(1)^2Y Simplify —— x 2 Equation at the end of step 1 y (((((x 2)(y 2))(z 2))(2x•——))y 2)z 2)2xz x 2 Step 2 Rewriting the whole as an Equivalent Fraction 21 Subtracting a fraction from a whole Rewrite the whole as a fraction using x as the denominatorApr 17, 12 · Use Lagrange Multipliers to find the extreme values of f subject to both constraints?



Practical Math 253 Chapter 15 Set 2 And 3 Studocu



Solved Let F X Y Z 1 X 2 Y 2 Z 2 Find The Domai Chegg Com
F(xy,z) = x 2 y 2 z The level surfaces are the parabaloids z = c x 2y 2 Example 4 Suppose we have f(x,y,t) = cos(t) e x 2 y 2 which represents the temperature at any pt on a rectangular plate in the plane At each fixed t 0 we have a function of 2 variables f(x,y,t 0) = cos(t 0) e x 2 y 2 For example below is the temperature profileClearly given f = (r^2)^(n) = r^(2n) where r = sqrt(x^2 y^2 z^2) = r Now as we know that grad(f) = f´(r) (r/r) ==> div(grad(f)) =div(f´(r) r/r)={grad(fF= ey2i(y sin(z2))j(z −1)k, and S is the upper hemisphere x 2 y 2 z 2 = 1, z ≥ 0, oriented upward Note that the surface S does NOT include the bottom of the hemisphere



Stoke S Theorem S Is The Part Of The Paraboloid Z X 2 Y 2 That Lies Insided The Parabaloid And Cyli Youtube



14 8 Lagrange Multipliers Ppt Download
A) \( \Large \phi \left(xyz, \frac{y}{z}\right)=0\) B) \( \Large \phi \left(\frac{y}{z},\frac{y}{x^{2}y^{2}z^{2}}\right) =0\) C) \( \Large \phi \left(\frac{y}{2Algebra Examples Rewrite (xy z)2 ( x y z) 2 as (xyz)(xyz) ( x y z) ( x y z) Expand (xyz)(xyz) ( x y z) ( x y z) by multiplying each term in the first expression by each term in the second expression Simplify each term Tap for more steps Multiply x x by x x Multiply y y by y yWith height 9 and base radius 2 that is centered about the zaxis with its base at z=2 Answer Save 1 Answer Relevance kb Lv 7 6 years ago Favorite Answer The cylinder has equation x^2 y^2 = 2^2, which can be rewritten as r = 2 in cylindrical coordinates As you stated, z is in



How To Compute The Gradient Of F X Y Z X 2 Y 3 Z 4 Youtube


Solved 6 Find The Maximum Value Of The Function F X Y Z Xyz On The Sphere X2 Y2 Z2 12 8 4 0 4 8 None Of These Rm 9 0 9 S 7 Maximi Course Hero
Nov 04, 13 · 1 Answer Let F (x, y, z) = x^2 y^9 y^2 z^3 x^8 z^7 2xyz = 5 So, ∂f (1,1,1)/∂x = 12/12 = 1 So, ∂f (1,1,1)/∂y = 13/12 = (2y^9 56x^6 z^7 56x^7 z^6 ∂z/∂x 2y ∂z/∂x) * (3y^2 z^2 7x^8 z^6 2xy)Check out a sample textbook solution See solution arrow_back Chapter 14, Problem 41RE Chapter 14, Problem 43RE arrow_forward Want to see this answer and more?So that u(x;y) = x x2 y2 and v(x;y) = y x2 y2 for z 6= 0 Now, @u @x = y2 x2 (x2 y2)2 = @v @y and @u @y = 2xy (x2 y2)2 = @v @x Since the partial derivatives are all continuous at each z 2 C;



Solved Suppose F X Y Z X2 Y2 Z2 And W Is The Sol Chegg Com



Answered 9 M A Y Z Xyz Xyz P 2 1 1 U Bartleby
F2 (x, y, z) = 2x^2 y^2 − 4z = 0 f3 (x,y,z) = 3x^2 −4yz^2 = 0 This system can be concisely represented as F (x) = 0, where F (x) = (f1, f2, f3)T , x= (x,y,z)T and 0 = (0,0,0)T (transpose written because these should be column vectors) Using matlabJul 04, 06 · Favorite Answer (xyz)^2 = (xyz) (xyz)= x^2y^2z^22xy2xz2yz => 1*1=32 (xyxzyz)=> 2 (xyxzyz)= 13 => xyxzyz =2/2 => xyxzyz = 1 Source (s) My little fuzzy brain Chunky 1 decade ago Man, all these variables must give you a headache!3Dplot of "x^2y^2z^2=1" Learn more about isosurface;


Solved Calculate S F X Y Z Ds Sf X Y Z Dsfor Y 3z 2 0x Z6 F X Y Z Z Y 3z2 0x Z6 F X Y Z Z S F X Y Z Ds Course Hero



Q 10 Show That The Expression X 2 Yz 3 Y 2 Zx 3 Z 2 Xy 3 3 X 2 Yz Y 2 Zx Z 2 Xy Is Youtube
But first, let's go to the gradient say v → = a b c x x 2 y 2 z 2 y x 2 y 2 z 2 z x 2 y 2 z 2 ⋅ a b c = x a y b z c x 2 y 2 z 2Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historySo how could we make things a bit easier



S Consists Of The Paraboloid Y X 2 Z 2 0 Y 1 And The Disk X 2 Z 2 1 Youtube



Chapter 16 1 16 3 Solutions Rogowski Pdf Document
Plot x^2 3y^2 z^2 = 1 Extended Keyboard;And the CauchyRiemann equations hold at each z 2 C;Given The force field is F (x,y,z) = (x−y2,y−z2,z−x2) F ( x, y, z) = ( x − y 2, y − z 2, z − x 2) and the particle moves along the line segment from (0,0,1) ( 0, 0, 1) to (2,1,0) ( 2



Math 53 Worksheet Solutions Minmax And Lagrange Pdf Free Download



Evaluate A Line Integral Of X 2 Y 2 Z 2 With Respect To Arc Length Mass Of Wire Youtube
Jun 16, 17 · Despite the fact that the same variables appear in every term, this expression does not factorize into one term There is no common factor, and no common bracket EAch term can be factored by differemce of squares xy(x^2y^2) yz(y^2z^2) zx(z^2x^2) =xy(xy)(xy) yz(yz)(yz) zx(zx)(zx) The only other option would be to multiply out the brackets and try aRewrite (x−y −z)2 ( x y z) 2 as (x−y−z)(x−y−z) ( x y z) ( x y z) Expand (x−y−z)(x−y−z) ( x y z) ( x y z) by multiplying each term in the first expression by each term in the second expression Simplify each term Tap for more steps Multiply x x by x x



Level Surfaces In Matlab
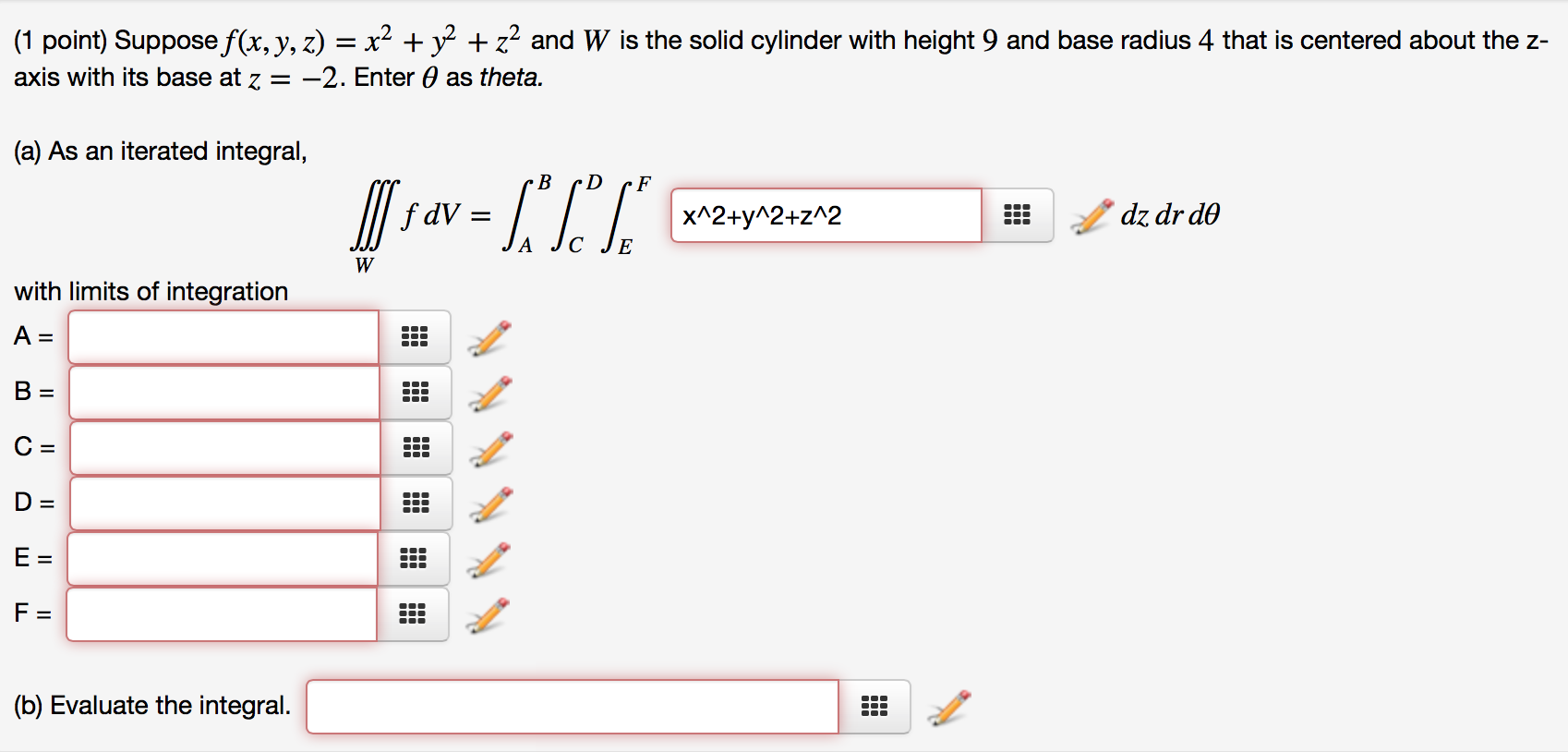


Solved Suppose F X Y Z X 2 Y 2 Z 2 And W Is The Solid Cy Chegg Com



Math 6c Chapter 12 Quiz



Let F Be A One One Function With Domain X Y Z And Range 1 2 3 It Is Given That Exactly Youtube



Functions Of Several Variables Ppt Download



File 2 Pdf Divergence Derivative



Solutions To Assignment 7
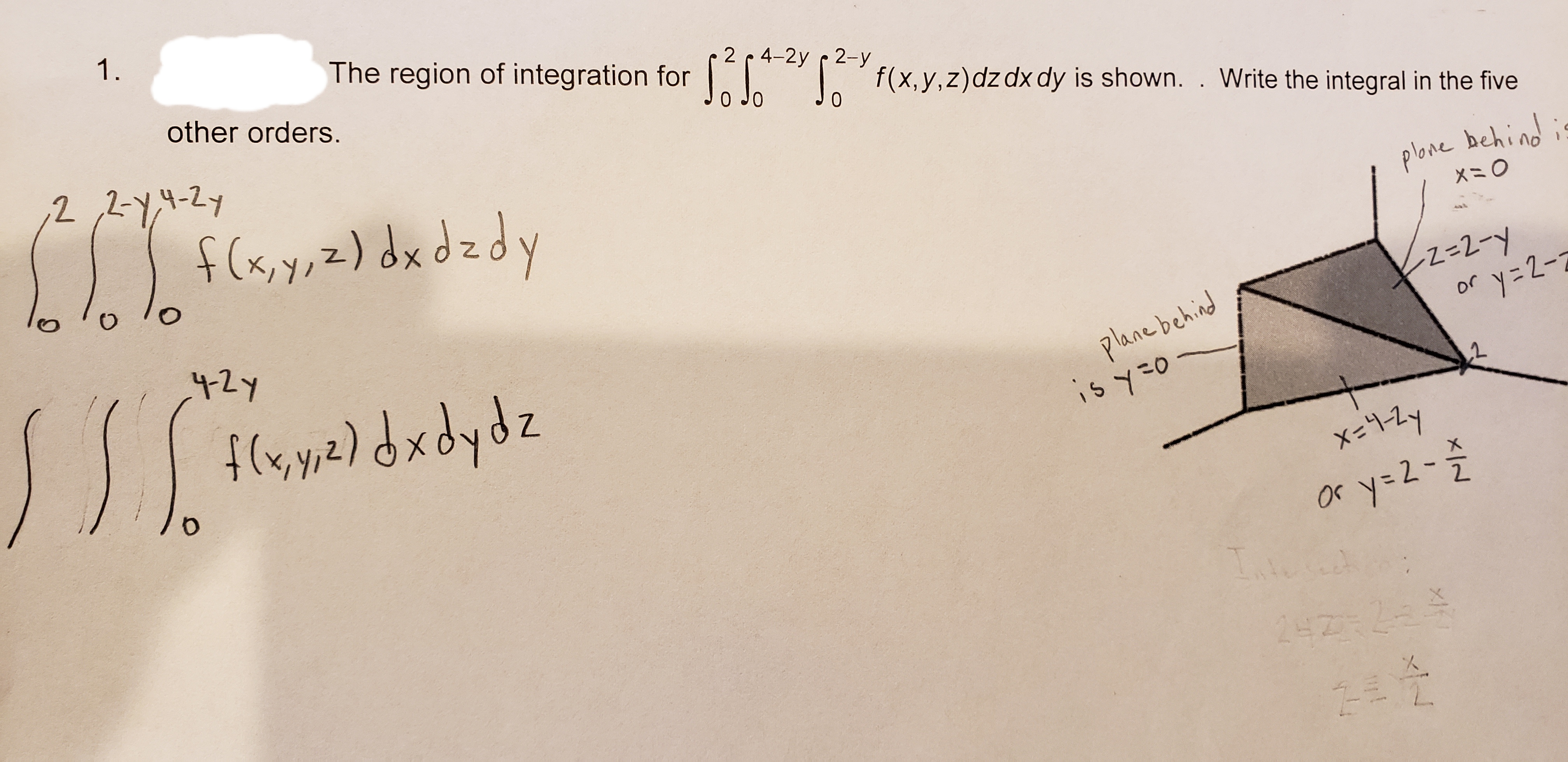


Answered 1 The Region Of Integration For F X Bartleby



Find The Total Differential Of The Multivariate Function F X Y Z E X Maths Exam Math Videos Calculus



Answered 14 F X Y Z X Y 4z X Y Bartleby



Solved Find The Maximum And Minimum Values Of The Functio Chegg Com


Chapter 7 Functions Of Two Variables Calculus And Analysis



Using Nabla With Partial Derivatives And The Laplace Operation Partial X 2 Partial Y 2 Partial Z 2 Mathematics Stack Exchange
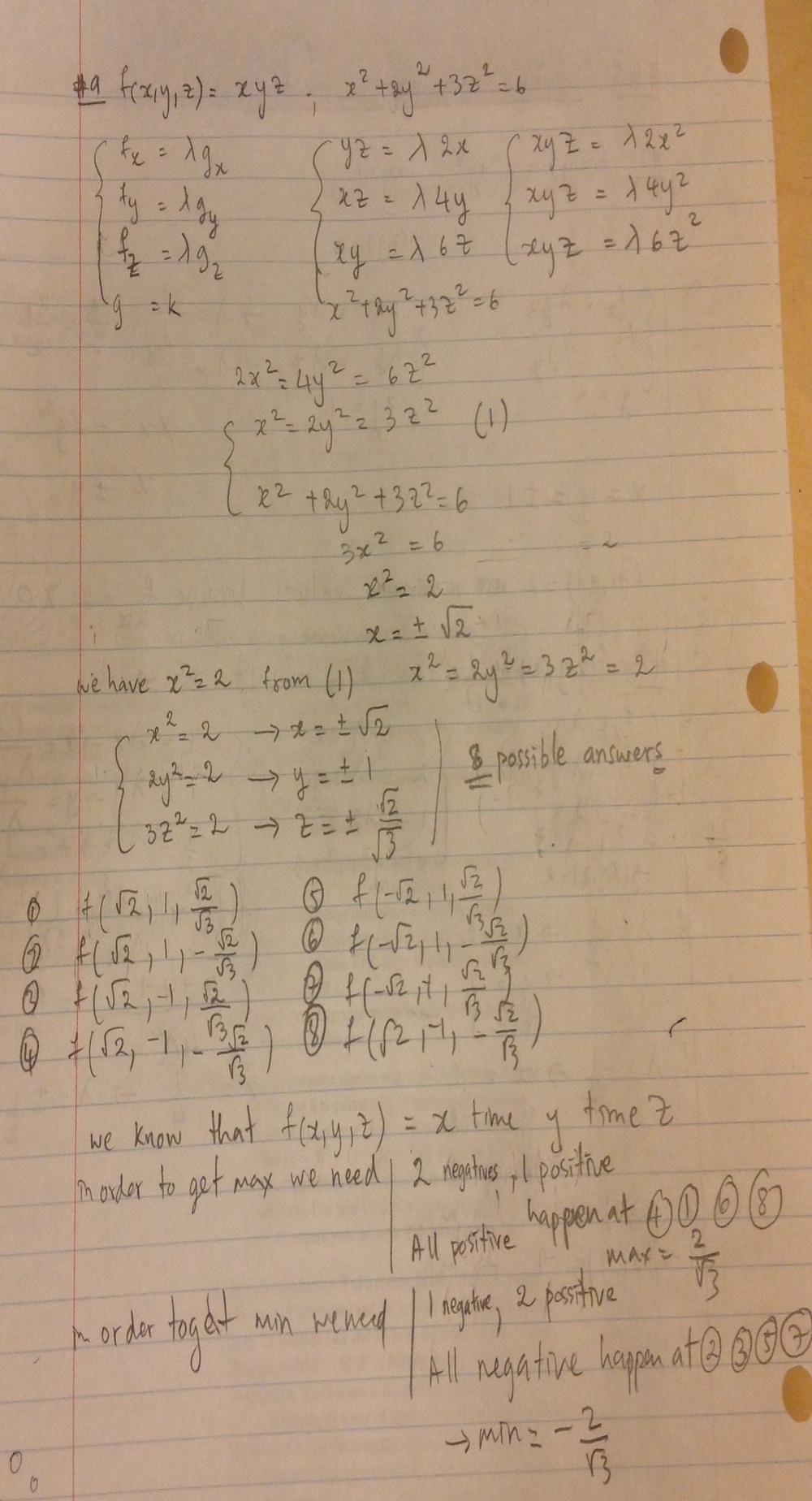


Use Lagrange Multipliers To Find The Maximum And Minimum Values Of The Function Subject To The Given Constraint F X Y Z Xyz X 2 2y 2 3z 2 6 Homework Help And Answers Slader
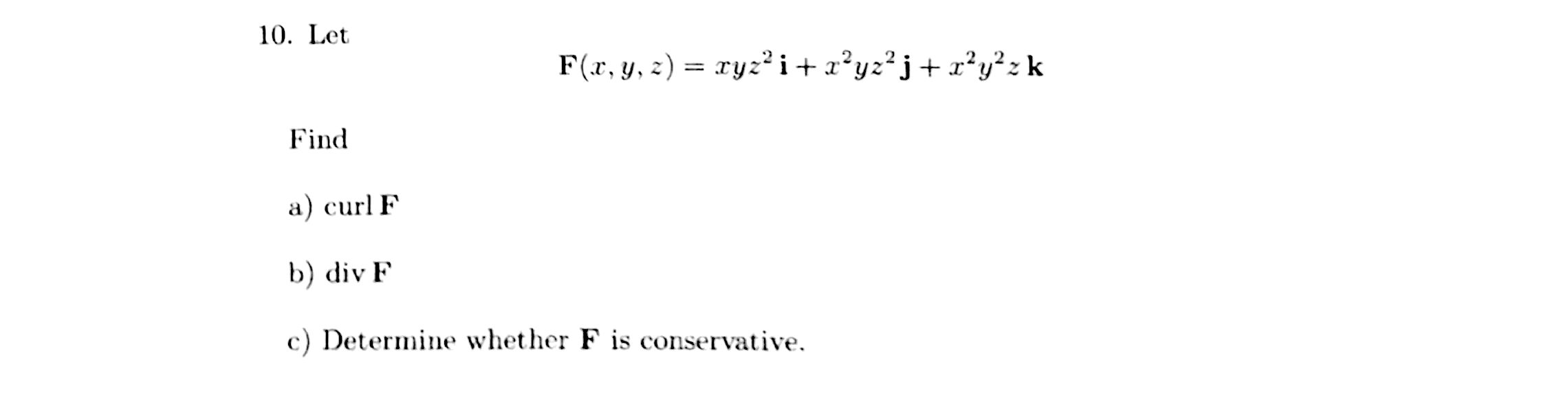


Solved Let F X Y Z Xyz 2 I X 2 Yz 2 J X 2 Y 2 Z Chegg Com



Level Surfaces In Matlab



Thomas Calculus 11e 8 1262 Pages 351 381 Flip Pdf Download Fliphtml5



1 Double Integrals Cankaya Universitesi Flip Ebook Pages 1 16 Anyflip Anyflip



Vector Calculus F X 2 Y 2 Z 2 3 2 X 2 Y 2 Z 2 3 2 X 2 Y 2 Z 2 3 2 Pdf Free Download
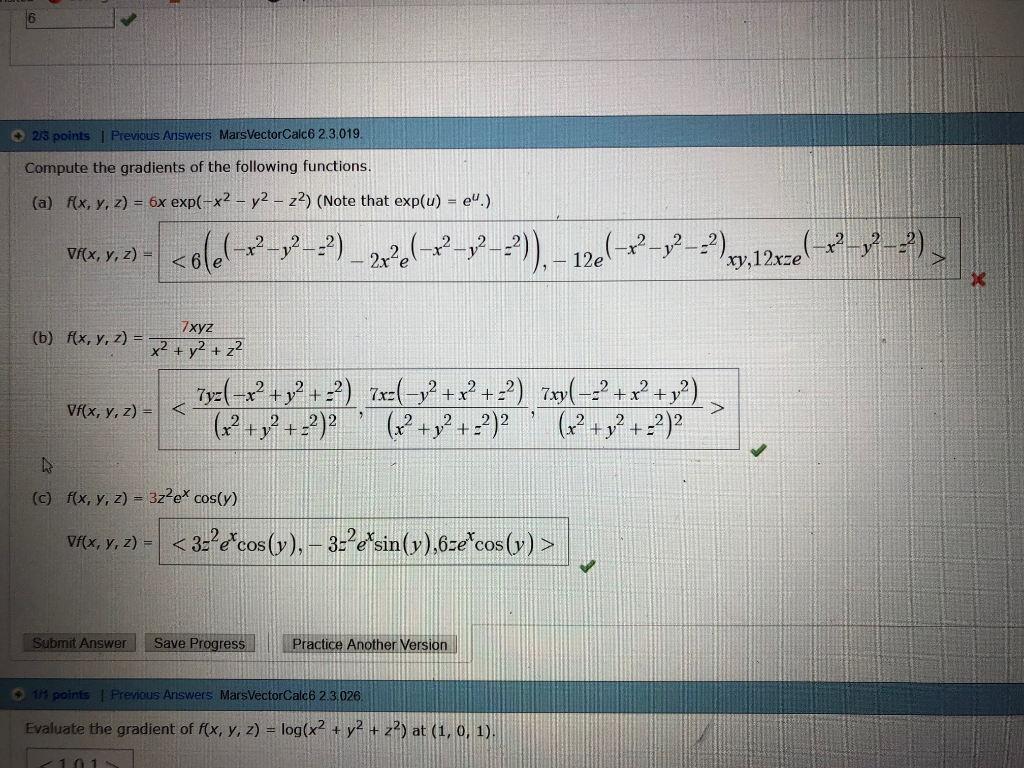


Solved 2 3 Points I Previous Answers Marsvectorcalc6 2 Chegg Com
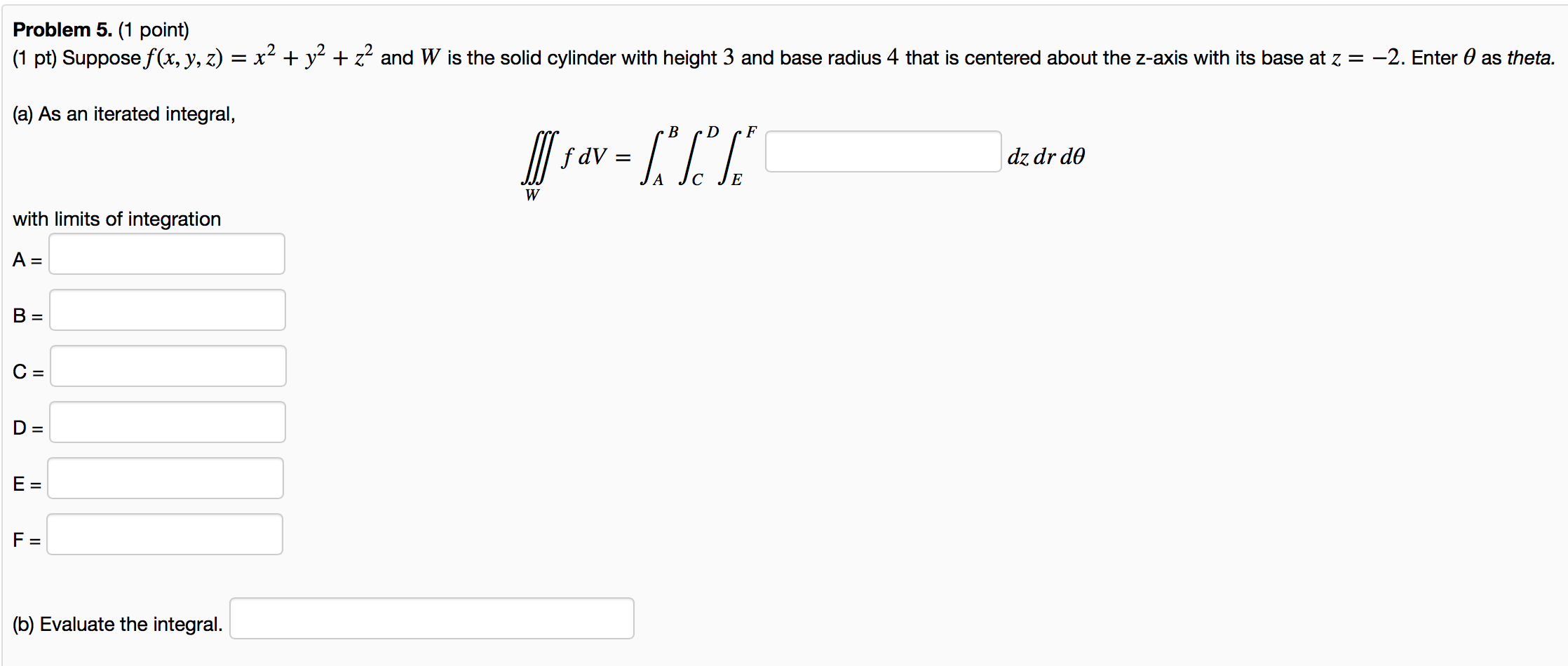


Solved Suppose F X Y Z X2 Y2 Z2 And W Is The Sol Chegg Com



Solved Let F X Y Z X 2 2yz 2 Xyz And G X Y Z Chegg Com



Find The Indicated Partial Derivatives Math F W X Y Z Sqrt X Y Y Z X 3 Sin Sqrt W 2 Z 2 F X X F Y Y F W X Y Z Math Homework Help And Answers Slader



Calc 501 1000 By James Bardo Issuu



Solved Determine If The Vector Field F X Y Z Xy 2 Z Chegg Com


Solved Find The Extreme Values Of F Subject To Both Constraints If An Answer Does Not Exist Enter Dne F X Y Z X 2y X Y Z 2 Y 2 Course Hero



0 件のコメント:
コメントを投稿